The image of an object can be made erect and much magnified by using more than one lenses. Therefore suitable combination of lenses are used in high powered optical instruments.
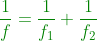
the above expression is for the combination of two lenses where f1 is the focal length of one lens and f2 is the focal length of the other.
a the above expression is for the combination of two lenses where f1 is the focal length of one lens and f2 is the focal length of the other.
In most of the optical instruments two or more lenses are used in combination. The location, size and nature of the final image can be determined by using lens formula or ray diagram. In either case, we locate first the image formed by the first lens. Using that image as the object for the second lens, the final image formed by the second lens can be located. If there are more than two lenses. This process is continued, the object for each lens is the image for the preceding lens as in the figure below:
 |
| Fig Showing a combination of thin lenses |
Referring to the above figure, we can see that lens L1 forms an image I1. This image acts as a real object for the lens L2, which forms a real image I2. Notice that I2 is inverted with respect to I1 and erect with respect to the object.
We now consider the case when the two thin lenses are in contact, which means their separation is very small as compared to their focal lengths. This is illustrated in figure below:
Let a point object O be placed at a distance p from the lens L1 whose real image I1(in fig I2) is formed by it at a distance q1(in fig q2). From the lens formula,
This image now serves as a virtual object for the second lens L2 of focal length f2. If we neglect the small separation between the lenses. The distance of this virtual object from lens L2 will be the same as its distance from the lens L1. If the lens forms an image I of this virtual object at a distance q.
Adding equation(1) and (2) we get,
Now if we replace the two lenses of focal lengths f1 and f2 by single lens of focal length f such that it forms an image at a distance q of an object placed at p from it as shown in figure below, such a lens is called equivalent lens, and its focal length is known as equivalent focal length.
For equivalent lens L, we have This close combination behaves as a single lens whose focal length is given by the above relation.
The equation(5) shows that for a pair of lenses in contact the sum of the reciprocals of their individual focal lengths is equal to the reciprocal of the focal length of the combination.


nice my friend
ReplyDeleteokay now ima start readin it .. wish me luck!
ReplyDeleteThis comment has been removed by the author.
DeleteThank you so much
ReplyDeleteGood work sir!.but there is some mistake in your 2nd diagram that is when first lens bending the light ray and when there is no second lens it bends again...this is impossible..this is major mistake
DeleteNice.but some mistakes .pls clear it.
ReplyDelete888 Casino Hotel NJ - JtmHub
ReplyDelete888 Casino Hotel is located 전라남도 출장마사지 in New Jersey and is part of the prestigious Resorts International Business 전주 출장샵 and Gaming Board Address: 777 강릉 출장샵 Casino Parkway, 김천 출장마사지 Atlantic City, 정읍 출장샵 NJ 08401Phone: 1-888-226-3340